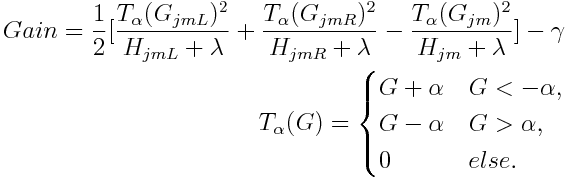In my previous blogs we have seen, decision trees and random forest. Now today, I will explore another very popular algorithm on Kaggle, which is XGBoost. It is currently the dominant algorithm for building accurate models on conventional data (also called tabular or strutured data).

XGBoost

Its name stands for eXtreme Gradient Boosting, it was developed by Tianqi Chen and now is part of a wider collection of open-source libraries developed by the Distributed Machine Learning Community (DMLC). XGBoost is a scalable and accurate implementation of gradient boosting machines and it has proven to push the limits of computing power for boosted trees algorithms as it was built and developed for the sole purpose of model performance and computational speed. Specifically, it was engineered to exploit every bit of memory and hardware resources for tree boosting algorithms. Read more

XGBoost is an implementation of the Gradient Boosted Decision Trees algorithm (scikit-learn has another version of this algorithm, but XGBoost has some technical advantages.)

How it differs from boosting algorithms GBM?

GBM divides the optimization problem into two parts by first determining the direction of the step and then optimizing the step length. Different from GBM, XGBoost tries to determine the step directly by solving:

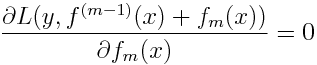
for each x in the data set. By doing second-order Taylor expansion of the loss function around the current estimate f(m-1)(x), we get

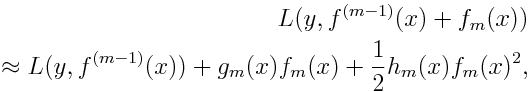
where g_m(x) is the gradient, same as the one in GBM, and h_m(x) is the Hessian (second order derivative) at the current estimate:

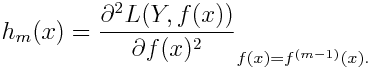
Then the loss function can be rewritten as

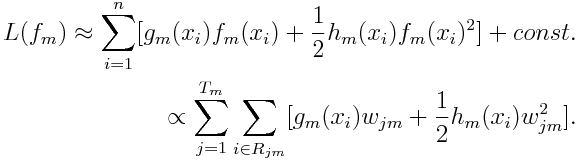
Letting G_jm represents the sum of gradient in region j and H_jm equals to the sum of hessian in region j, the equation can be rewritten as

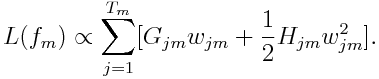
With the fixed learned structure, for each region, it is straightforward to determine the optimal weight :

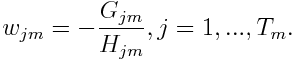
Plugging it back to the loss function, we get

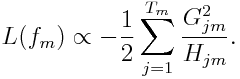
According to Chen, this is the structure score for a tree. The smaller the score is, the better the structure is. Thus, for each split to make, the proxy gain is defined as

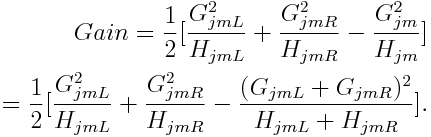
Well, all deductions above didn’t take regularization into consideration. Note that XGBoost provides variety of regularization to improve generalization performance. Taking regularization into consideration, we can rewrite the loss function as

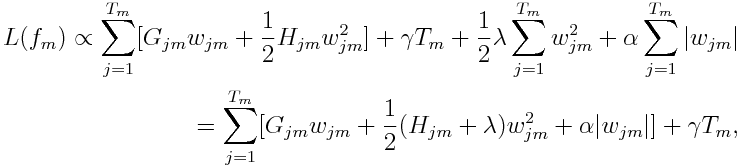
where γ is the penalization term on the number of terminal nodes, α and λ are for L1 and L2 regularization respectively. The optimal weight for each region j is calculated as:

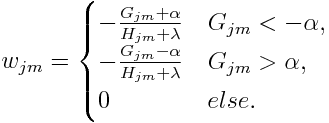
The gain of each split is defined correspondingly:

Read more